【Leetcode】322.零钱兑换

322 零钱兑换

题目

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3 
解释: 11 = 5 + 5 + 1

示例 2:
输入: coins = [2], amount = 3
输出: -1

方法（暴力递归）

如果想求 amount = 11 时的最少硬币数（原问题），若已经知道凑出 amount = 10 的最少硬币数（子问题），你只需要把子问题的答案加一（再选一枚面值为 1 的硬币）就是原问题的答案。因为硬币的数量是没有限制的，所以子问题之间没有相互制约，是互相独立的。

按如下步骤来考虑：

  1. 分析base case：当目标金额 amount 为 0 时算法返回 0，因为不需要任何硬币就已经凑出目标金额了。

  2. 分析可变参数，也就是原问题和子问题中会变化的变量。由于硬币数量无限，硬币的面额也是题目给定的，只有目标金额会不断地向 base case 靠近，所以唯一的可变参数就是目标金额amount。

  3. 确定决策，也就是导致可变参数产生变化的行为。目标金额为什么变化呢，因为你在选择硬币，你每选择一枚硬币，就相当于减少了目标金额。所以说所有硬币的面值，就是你的决策。

  4. 明确 dp 函数/数组的定义。如果是自顶向下的暴力递归情况，就会有一个递归的dp函数，一般来说函数的参数就是状态转移中会变化的量，也就是上面说到的可变参数；函数的返回值就是题目要求我们计算的量。

    就本题来说，可变参数只有一个，即「目标金额」，题目要求我们计算凑出目标金额所需的最少硬币数量。所以我们可以这样定义 dp 函数：dp(n) 的定义：输入一个目标金额 n，返回凑出目标金额 n 的最少硬币数量。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int coinChange(int[] coins, int amount) {
        return dp(coins, amount);
    }
    //编写dp函数，它对于一个要凑成的总金额，返回最少用的硬币个数
    public int dp(int[] coins, int amount){
        if(amount == 0)
            return 0;
        if(amount < 0)
            return -1;
        int res = Integer.MAX_VALUE;
        for(int coin: coins){
            int subProblem = dp(coins, amount - coin);
            if(subProblem == -1)
                continue;
            res = Math.min(res, 1 + subProblem);
        }
        return res != Integer.MAX_VALUE ? res : -1;
    }
}

方法（动态规划）

以上暴力解法的代码转化为数学形式就是状态转移方程：

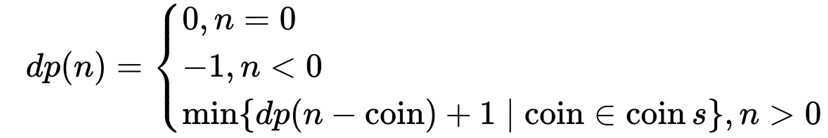
上述的暴力递归方法是自顶向下的，因此会产生很多重复计算。我们接下来把它改成自底向上的动态规划：

动态规划需要一个dp数组，dp数组的定义与上述的dp函数类似，其索引是要凑成的金额amount的值，索引对应的值为要凑成amount需要的最小硬币数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int coinChange(int[] coins, int amount) {
    int[] dp = new int[amount + 1];
    //将dp数组的所有元素初始化为amount + 1，因为dp[amount] 最大不可能超过 amount（最小面值为 1 元），所以 amount + 1 是一个无意义的数。
    //如果索引index对应的数组元素为amount + 1，代表无法通过给定的硬币凑成金额index。
    Arrays.fill(dp, amount + 1);
    dp[0] = 0;
    for(int i = 0; i < dp.length; i++){
        //计算dp[i]：要凑成金额i最少需要多少硬币
        for(int coin : coins){
            if(i - coin < 0)
                continue;
            dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
        }
    }
    return (dp[amount] == amount + 1) ? -1 :dp[amount];
}