【Leetcode】450.删除二叉搜索树中的节点

450.删除二叉搜索树中的节点

题目

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

示例:
root = [5,3,6,2,4,null,7]
key = 3

    5
   / \
  3   6
 / \   \
2   4   7

给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。

一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。

    5
   / \
  4   6
 /     \
2       7

另一个正确答案是 [5,2,6,null,4,null,7]。

    5
   / \
  2   6
   \   \
    4   7

方法

若要在一颗根为root的二叉搜索树中删除值为key的节点，一共有三种情况：

  1. key < root.val
    由于二叉搜索树左子树的节点值都小于根节点，因此值为key的节点一定位于左子树中，我们递归在左子树中删除值为key的节点，并将删除结束后的新的左子树与根节点连接即可。

  2. key > root.val
    由于二叉搜索树右子树的节点值都大于根节点，因此值为key的节点一定位于右子树中，我们递归在右子树中删除值为key的节点，并将删除结束后的新的右子树与根节点连接即可。

  3. key = root.val
    当key与根节点值相等时，意味着要删除的节点正是根节点root自己。于是可以分两种情况讨论：

    • 若root的右子树为空，则要想删除root节点，只需让root的左子树替代它的位置即可。
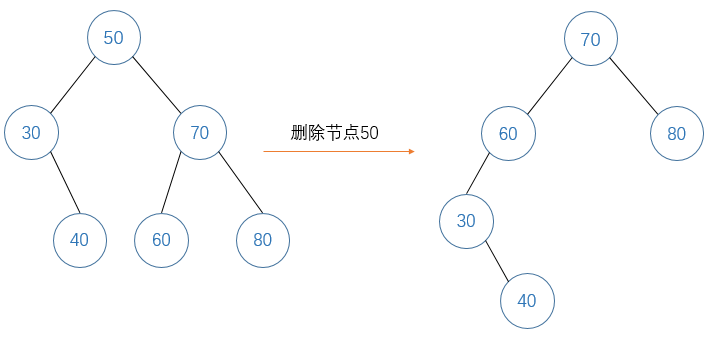
    • 若root的右子树不为空，由于右子树中最左的节点即为右子树中值最小的节点，root左子树的所有节点都比这个节点小，因此我们只要找到右子树中这个最左的节点，将root的左子树挂到它下面，成为它的左子树即可。如下图所示：将50的左子树挂到50的右子树的最左的节点60下，成为60节点的左子树

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public TreeNode deleteNode(TreeNode root, int key) {
    if(root == null)
        return null;
    //情况一：在root的左子树中删除值为key的节点
    if(key < root.val){
        TreeNode L = deleteNode(root.left, key);
        root.left = L;
    }
    //情况二：在root的右子树中删除值为key的节点
    else if(key > root.val){
        TreeNode R = deleteNode(root.right, key);
        root.right = R;
    }
    //情况三：删除root节点自身
    else{
        if(root.right == null)
            return root.left;
        else{
            //用cur找到root右子树中最左的节点
            TreeNode cur = root.right;
            while(cur.left != null)
                cur = cur.left;
            //将root的左子树挂到这个节点之下
            cur.left = root.left;
            return root.right;
        }
    }
    return root;
}