514.自由之路

题目

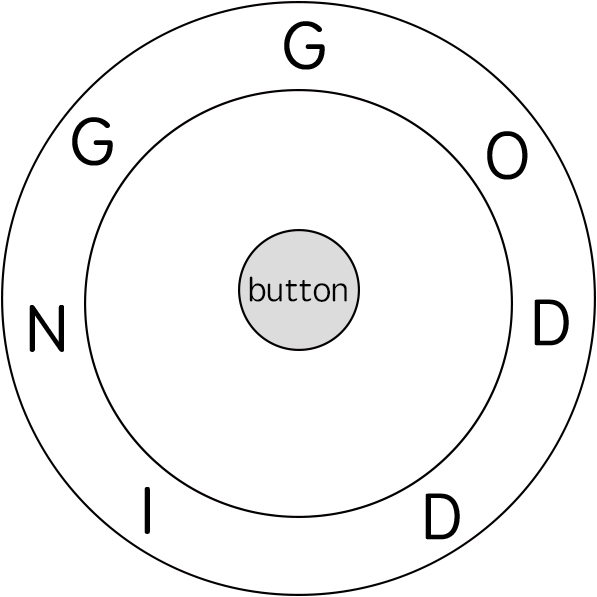
视频游戏“辐射4”中，任务“通向自由”要求玩家到达名为“Freedom Trail Ring”的金属表盘，并使用表盘拼写特定关键词才能开门。

给定一个字符串 ring，表示刻在外环上的编码；给定另一个字符串 key，表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。

最初，ring 的第一个字符与12:00方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐，然后按下中心按钮，以此逐个拼写完 key 中的所有字符。

旋转 ring 拼出 key 字符 key[i] 的阶段中：

• 您可以将 ring 顺时针或逆时针旋转一个位置，计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐，并且这个字符必须等于字符 key[i] 。
• 如果字符 key[i] 已经对齐到12:00方向，您需要按下中心按钮进行拼写，这也将算作 1 步。按完之后，您可以开始拼写 key 的下一个字符（下一阶段）, 直至完成所有拼写。

示例：

输入: ring = "godding", key = "gd"
输出: 4
解释:
对于 key 的第一个字符 'g'，已经在正确的位置, 我们只需要1步来拼写这个字符。 
对于 key 的第二个字符 'd'，我们需要逆时针旋转 ring "godding" 2步使它变成 "ddinggo"。
当然, 我们还需要1步进行拼写。
因此最终的输出是 4。

方法一（暴力递归）

记dfs(i,j)为从ring的i位置出发，拼写出key的j位置及其之后所有字符（key[j….])，所需要走的最少步数是多少。

因为字符串 key 一定可以由字符串 ring 旋转拼出。因此当key已经拼完时（j等于key.length）为递归函数的返回条件。此刻返回0，因为key已全部拼完，不需要再走步数了。

当key尚未拼完时，我们若要从ring的i位置出发，拼写出key的j位置及其之后所有字符，需要走的步数包含两部分：

1. 拼出key中j位置的字符：由于ring中可能有重复字符，因此key[j]在ring中可能有多个出现的位置，我们选择一个最近的位置，转distance步，使得ring中12：00方向指向一个与key[j]相等的字符，然后按下中心按钮，拼出这一字符，于是这一部分要走distance+1步。
2. 拼出key中j位置之后的所有字符：我们需要在ring中从刚才转distance步到达的这个位置开始，拼出key中从j+1位置开始的字符。递归求这一部分要走的步数：dfs(next, j + 1)

因此一共要走distance+1 + dfs(next, j + 1)步。

String ring;
String key;
Map<Character, List<Integer>> map;
public int findRotateSteps(String ring, String key) {
    this.ring = ring;
    this.key = key;
    //map的key为字符，value为字符在ring中出现的位置（一个字符可以出现多次，因此value为列表）
    map = new HashMap<>();
    for(int i = 0; i < ring.length(); i++){
        char ch = ring.charAt(i);
        if(!map.containsKey(ch))
            map.put(ch, new ArrayList<>());
        map.get(ch).add(i);
    }
    return dfs(0, 0);
}

public int dfs(int i, int j){
    if(j == key.length())
        return 0;
    int min = Integer.MAX_VALUE;
    for(int position : map.get(key.charAt(j))){
        //转到key[j]字符有顺时针转和逆时针转两种转法，我们采用步数较小的那种
        int forwardDist = Math.abs(i - position);
        int backDist = ring.length() - forwardDist;
        int distance = Math.min(forwardDist, backDist);
        min = Math.min(min, distance + 1 + dfs(position, j + 1));
    }
    return min;
}

方法二（动态规划）

暴力递归改动态规划一共有如下几步：

1. 分析哪几个可变参数可以确定返回值的状态。对于这道题：ring中的位置i和key中的位置j一旦确定，返回值就确定
2. 分析参数的变化范围，建立dp数组（可变参数有几个，dp数组就是几维）。于是:

   int[][] dp = new int[ring.length()][key.length()];

3. 根据暴力递归的递归结束条件，确定base case

   //Base Case:j为key.length() - 1时
   for (int i = 0; i < ring.length(); i++) {
       int min = Integer.MAX_VALUE;
       for (int position : map.get(key.charAt(key.length() - 1))) {
           int forwardDist = Math.abs(i - position);
           int backDist = ring.length() - forwardDist;
           int distance = Math.min(forwardDist, backDist) + 1;
           min = Math.min(min, distance);
       }
       dp[i][key.length() - 1] = min;
   }

4. 根据递归主体，分析出一个普遍位置是怎么依赖的。然后依次填充dp数组

代码

String ring;
String key;
Map<Character, List<Integer>> map;
public int findRotateSteps(String ring, String key) {
    this.ring = ring;
    this.key = key;
    //构建map，这步和暴力递归解法相同
    map = new HashMap<>();
    for (int i = 0; i < ring.length(); i++) {
        char ch = ring.charAt(i);
        if (!map.containsKey(ch))
            map.put(ch, new ArrayList<>());
        map.get(ch).add(i);
    }
    //构建dp数组
    int[][] dp = new int[ring.length()][key.length()];
    //确定Base Case:j为key.length() - 1时
    for (int i = 0; i < ring.length(); i++) {
        int min = Integer.MAX_VALUE;
        for (int position : map.get(key.charAt(key.length() - 1))) {
            int forwardDist = Math.abs(i - position);
            int backDist = ring.length() - forwardDist;
            int distance = Math.min(forwardDist, backDist) + 1;
            min = Math.min(min, distance);
        }
        dp[i][key.length() - 1] = min;
    }
    //填充dp数组
    for (int j = key.length() - 2; j >= 0; j--) {
        for (int i = 0; i < ring.length(); i++) {
            int min = Integer.MAX_VALUE;
            for (int position : map.get(key.charAt(j))) {
                int forwardDist = Math.abs(i - position);
                int backDist = ring.length() - forwardDist;
                int distance = Math.min(forwardDist, backDist);
                min = Math.min(min, distance + 1 + dp[position][j + 1]);
            }
            dp[i][j] = min;
        }
    }
    return dp[0][0];
}